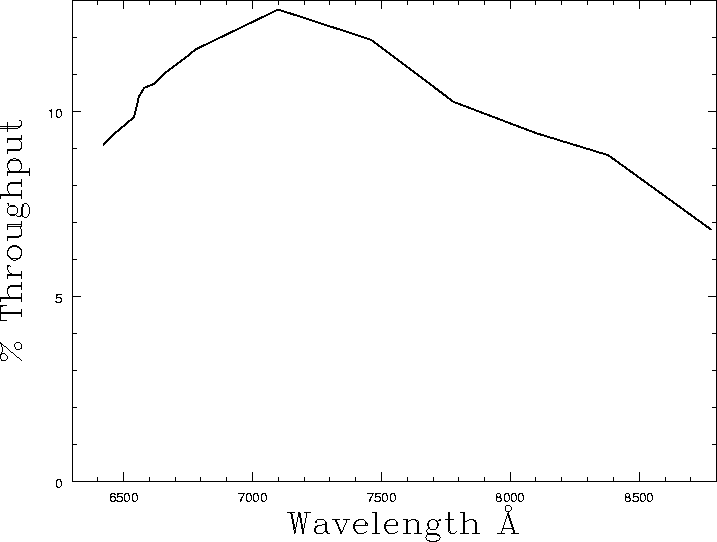
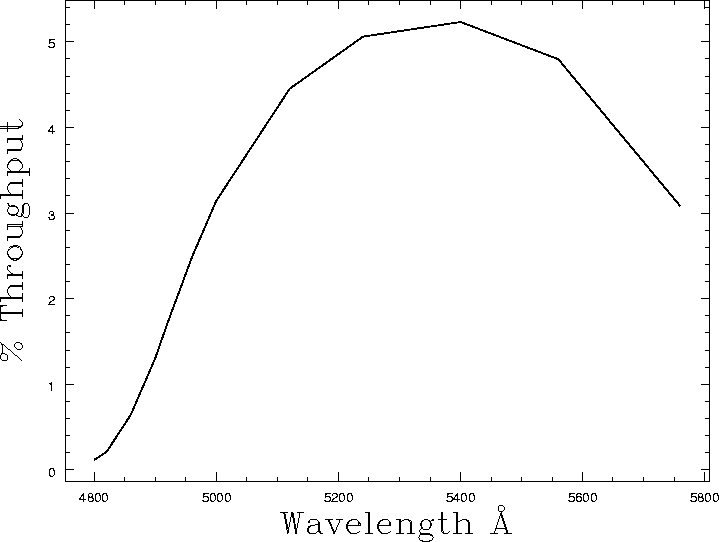
LRS Throughput

It is important for the PI to realize that due to the design of the HET the effective collecting area changes over a trajectory. Near the end of a trajectory the HET has half the collecting area in comparison to the middle of a trajectory. As such two medium length visits centered on middle of a track are sometimes more valuable than a single long visit. All Throughput estimates are based upon center of track throughputs.

We have no imaging performance benchmarks yet because the depth depends so much on image quality and sky brightness.

Rough Estimates

These are sky noise dominated observations, so remember to scale by the sqrt(time).
ALL S/N are per assuming 2x2 binning and are per resolution element.

Configuration Type of Object Mag. Time S/N @ Wavelength

LRS_g1_2.0_GG385 stellar/QSO 20 1800 15-20 @ 6500 Å

LRS_g1_2.0_GG385 stellar/QSO 21 1800 3-8 @ 6500 Å

LRS_g1_2.0_GG385 distant galaxy 21 1800 9-14 @ 6500 Å

LRS_g2_2.0_GG385 distant galaxy 21 1800 4-9 @ 6500 Å

LRS_e2_1.0_E2F stellar 20 1800 8-12 @ 5000 Å

Configuration	Type of Object	Mag.	Time	S/N @ Wavelength
LRS_g1_2.0_GG385	stellar/QSO	20	1800	15-20 @ 6500 Å
LRS_g1_2.0_GG385	stellar/QSO	21	1800	3-8 @ 6500 Å
LRS_g1_2.0_GG385	distant galaxy	21	1800	9-14 @ 6500 Å
LRS_g2_2.0_GG385	distant galaxy	21	1800	4-9 @ 6500 Å
LRS_e2_1.0_E2F	stellar	20	1800	8-12 @ 5000 Å

If you find these values to be incorrect over a significant data set PLEASE send us your better estimation and what program number this data comes from.

To see the affect of changing exposure times in a moving aperature try the HET Filling Factor Calculator.

Throughput

In the following plots we give the throughput for each grating assuming a 9.2m telescope with a 3.713m obstruction, observed right at the center of the track (see fill factor information for more on this) and corrected to above the atmosphere using the KPNO extinction coefficients Click on the plot to download the text file used to generate the plot.

LRS g1

LRS g2

LRS g3 now defunct

LRS e2

All LRS grisms

Using this Data

To properly use this data the investigator should calculate the number of photons incident on a 9.2m aperature with a 3.713m obstruction (55.6 square meters of collecting area) from their source. Multiply by the system throughput at the wavelength of interest for the configuration of interest. Correct for extinction (a typical airmass for the HET is 1.2). This gives the number of photons you should expect without slit losses per wavelength unit. Multiply by the resolution element width to get the photons per RE. Correct for the slit losses by assuming a typical seeing (say 2.0") and your slit configuration of interest. This is still assuming perfect sky transmission (ie photometric which occurs only ~25% of the time). To correct to typical spectroscopic conditions remove ~20% of the photons. The sqrt of this number gives you the S/N in the absense of sky noise (the largest noise source). Include a sky noise term by scaling the preslit photons by the relative magnitudes of the target and the sky (never fainter than 21.0) and multiplying by the slit width in arcseconds. Add the noise sources in quaderature and divide into your source flux. See simple! Or just use the rough estimate at the top of the page.