Multidimensional Dynamic Arrays

Modules

Multidimensional Dynamic Arrays

Terminology

LTL currently provides dynamic arrays of up to 7 dimensions (this is not a principle limitation. Higher dimensions are easily possible, I'm just too lazy to create higher dimensional versions of the needed methods. If you need them, feel free ...). The class' declaration is 

template<class T, int N> class MArray;

T is the type stored in the array, and N is the number of dimensions, so, for example, 

MArray<float,2> Image(1024,1024);

represents a 2 dimensional array holding 1024 times 1024 floats.

The terminology used is as follows:

Utility classes

The Class Range

A Range is a utility object used in the context of MArray describing a range of integers used for creating arrays and indexing an array along one dimension. See the Range class reference documentation range.h.

The Class FixedVector

This class is used to hold lists of indices for referencing arbitrary sets of elements of an MArray, e.g. the list of elements of a matrix which are ==0.

The Class MArray

template<class T, int N> class MArray;

This is LTL's main class. It represents a dynamic multidimensional array. The template parameters T specifies the type of objects stored in the array and the template parameter N specifies the rank, i.e. the number of dimensions. Therefore, MArray<float,2> represents a two-dimensional array holding floats. Note that only the number of dimensions of the MArray are templated. The actual size of each dimension is determined at runtime. Include <ltl/marray.h> to use this class.

MArrays feature subarrays (sometimes called views), slices, expression templated evaluation, and other features described below. The memory holding the actual data is reference counted, such that it is not freed until the last reference to the data by views or slices has been removed.

MArrays use column-major storage (fortran storage order). For matrices, this means that adjacent elements in memory hold values from the same row. For images, the first index refers to neighboring pixels in an image line. The first (leftmost) index has the smallest stride, the last (rightmost) index has the largest stride.

(Note: For not too large one or two-dimensional arrays (i.e. vectors and matrices) whose size is known at compile-time, you might prefer to use the classes FVector and FMatrix.)

Creating MArrays

See MArray::MArray for a full description of all constructors. Here we just give some code examples.

// 3-dim array with indices ranging from 1 to 128
MArray<float,3> A(128,128,128);

// 2-dim array with indices -10,9,...,9,10 along dimension 1
//                      and  21,23,...,29  along dimension 2
MArray<float,2> B( Range(-10,10), Range(21,29,2) );

// new 3-dim array of same geometry as A
MArray<float,3> C( A.shape() );

// construct from expression
// new array gets the geometry of the expression
// the following 2 statements are absolutely equivalent
MArray<float,2> D = -2.5 * log(B);
MArray<float,2> D( -2.5 * log(B) );

// construct an array without allocating memory. Memory can be allocated later
// using makeReference() or using assignment.
MArray<float,2> E;

The copy constructor and operator=()

The copy constructor 

MArray<T,N>::MArray( const MArray<T,N>& other );

Note that other's data are NOT copied. The copy constructor only references the other array's data. This is for allowing functions to return MArray objects in an efficient manner. Use operator= to copy the content of arrays.

MArray::operator= is the only way to copy data from one MArray to another. All other methods (copy construction, initialization assignment) only create references (see MArray::makeReference()). MArray::operator= also allows for uninitialized lhs MArrays with MArray or expression rhs. In this case memory to hold the result is allocated and the MArray filled with a copy of the rhs MAarray or the evaluated values of the expression. If the lhs MArray already has memory allocated, then the lhs and rhs shapes have to be conformable.

Uninitialized MArrays

It is legal to declare an MArray object without specifying the extents of its dimensions. Such MArrays are said to be uninitialized. They are useful as class members which are filled with an amount of data unknown at the time of construction. It is legal to call operator= and the copy-constructor on uninitialized arrays (so that a class instance containing an uninitialized MArray member can be passed and copied). It is not legal to assign an expression involving uninitialized operands. This should be caught when LTL_RANGE_CHECKING is used. If the lhs of an assignment is uninitialized but the rhs is not, the lhs will allocate memory to hold the result of evaluating the rhs. The other method of allocating memory to an uninitialized MArray is using MArray::makeReference(). In this case, the data is not copied, but the uninitialized MArray becomes a view of another MArray's data.

Indexing MArrays

Indexing an array can yield a single element (scalar) or a subarray/slice combination. Indexing is generally done using operator(). Providing only int arguments to operator() yields a scalar (or a reference to a scalar), any combination of int arguments and Range objects yields a subarray/slice. (See also the MArray class reference documentation on MArray::operator().) For flipping, rotating, reversing or transposing arrays have a look at MArray::reverse(), MArray::reverseSelf(), MArray::transpose(), and MArray::transposeSelf().

Range objects can have non-unit strides, in which case the subarray/slice refers to every k-th element of the in the specified range along the original array dimension.

Note that if array-valued indexing is performed, the returned subarray or slice is referencing the original array's data. No copying is performed. Additionally, an array can be indexed using an IndexList object, which is a collection of an arbitrary set of array elements, returned by the function where().

Indexing is always performed using MArray::operator(). Here are some examples:

MArray<float,2> M( 100, 100 );
MArray<float,3> C( 100, 100, 100 );
float a, b;

// Indexing a single element
//    Note that we are using column major storage:
//    The first index refers to adjacent elements in memory, the last index
//    has the largest stride.
a = M(34,23);

// scalar assignment
M(12,87) = a;

// assignment of a scalar to a subarray (all elements = a)
// with non-unit strides (every second element in the first dimension
// and every third element in the second dimension
M( Range(25,50,2), Range(25,50,3) ) = a;

// assignment of a slice to a subarray
M( Range(25,50), Range(25,50) ) = C( 1, Range(75,100), Range(75,100) );

// indexing a slice (the 5th column)
// and initializing a new array with the slice
// calls the copy-constructor NOT operator=, so that Column becomes
// a view of M (it references M's data)
MArray<float,1> Column = M( 5, Range::all() );

Note that the index base of a subarray is reset to 1. Thus in the example above the submatrix has ranges 1..25 and 1..25. See method MArray<T,N>::setBase() if you need to change the base index.

Formally, we have the following variants of MArray::operator() 

   T  MArray<T,N>::operator()( int n1, ..., int nN ) const
   T& MArray<T,N>::operator()( int n1, ..., int nN )
   T  MArray<T,N>::operator()( const FixedVector& i ) const
   T& MArray<T,N>::operator()( const FixedVector& i )

Index an MArray to obtain a single element of the array. The forms returning T& are provided such that indexing expressions can be used on the lhs of assignments.

MArray<T,N> MArray<T,N>::operator()( Range R1, ..., Range RN )

Return a subarray (an array having the same rank, but referring to a subset of the original array) of the original array. The returned MArray references the original array's data, so modifying the subarray's data modifies the original array's data.

Reference counting is performed on the actual data blocks, so the user does not have to worry about arrays going out of scope or being deliberately deleted while references still exits.

 MArray MArray<T,N2>::operator()( [any combination of int and Range arguments] )

This actually has the simplified form 

template<int N2>
template<some wild stuff...>
MArray<T,N2> operator()( [any combination of int and Range args] )

Return a slice of the original array. The returned MArray references the original array's data, so modifying the subarray's data modifies the original array's data. Again, reference counting is performed.

Hereby the rank of the created array is reduced by 1 compared to the original array for every int argument given in the call (we say the dimension is "sliced away"). One could slice a 3-dimensional cube to get a matrix (using 1 int and 2 Range arguments) or a vector (using 2 int arguments and one Range argument) and so on ...

Additionally, there is the IndexList, which refers to an arbitrary set of elements:

MArray<float,3> A(nx,ny,nz);

A = ...;

// set all zeros to 1
IndexList<3> list = where( A==0 );
A[list] = 1;   // or any conformable 1-d expression

Note that operator() is used to return a 1-d array of values by indexing an arbitrary geometry array with an index list, while operator[] is used to return a special object hoving an operator= so that one can assign a 1-d array to an arbitrary set of indices from an index list.

We have used the function 

IndexList<N> where( [some N-dim boolean expression] );

Specifically, MArray provides

MArray MArray<T,1>::operator()( const IndexList<N>& l )

Subscript an N-dimensional MArray with an list of indices, returning a 1 dimensional MArray.

MArray IndexRef<T,N>::operator[]( const IndexList<N>& l )

Returns an IndexRef<T,N> object, which has an operator= implementation such that the the expression A[list] can be used on the lhs of an assignment.

Assignment

Assignment to array elements or to whole arrays (or subarrays) is straightforward. Assignment is always possible from a scalar expression, in which case the whole left-hand side (lhs) (if it is not a scalar reference itself) is filled with the scalar value, i.e. A=0; will set all elements of array A to 0.

Assignment to an array (no matter if it is a subarray or a slice of another array or not) is possible from scalars, arrays (or subarrays or slices), and from array-valued expressions. In the case that the rhs of the assignment is array-valued, the lhs and the rhs have be conformable. Array and Expression Conformability, for further details.

A few examples: 

MArray<float,2> A(n1,n2), B(n1,n2), C(n1,n2);
A=0; // all of A = 0;
B=C=2.222;

A = (sin(B) + C/2) * exp( -(C*C) ); // assignment from expression

// assignment to slice from expression with slice
A( 2, Range(10:20) ) = 5 + log( B( 4, Range(1:10) ) / 3. );

The only important thing to note here is that assignment copies the data while initialization/construction from another array object only references the other array's data.

To ease initialization of arrays, a handy method is provided using a comma-delimited list of values: 

MArray A(4,4);

A = 1,  0,  0,  0,
    0, -1,  0,  0,
    0,  0, -1,  0,
    0,  0,  0, -1;

Note, though, that since MArrays have fortran storage order (column major storage), the above actually fills the array with the transpose of what's written there.

Element types of MArrays

As of LTL version 1.0, arbitrary data types are supported as MArray elements, as long as a default constructor and a copy constructor are provided. Support for such data types in LTL versions 2.0 and later is much more complete. In LTL 2.0 and later, if the data type provides arithmetic operators and/or mathematical operators, then expression templates will also work out of the box. In particular, LTL 2.0 and later supports MArrays of complex<float> and complex<double>, FVector, and FMatrix with full expression template support and mathematical operations and operators:

The follwing code fragments show some examples of what's allowed in LTL 2.0 and later:

// MArray<FVector> example:
MArray<FVector<float,3>, 1> A(10), B(10);
FVector<float,3> v, w, zero;
v = 1,2,3;   w = 3,6,9;    zero = 0;
A = 2.0f*v + w;
B = A+2*A;
B = 2*A-2*w;

// Gradient example showing mixed expressions:
MArray<float,2> A(10,10);                 // a scalar field
MArray<FVector<float,2>,2> B(10,10);      // it's gradient is a vector field
A = ...
B = convolve(A,grad2D());

Iterators

Iterators are "generalized pointers" to the elements of an array of arbitrary geometry, providing two operations, namely dereferencing via operator* (returning the value of the element currently pointed to or a reference to it for use on the rhs) and moving the "pointer" to the next element via operator++.

They are very useful for implementing the probably most common pattern applied to arrays in scientific computing - doing something for all elements of an array (and thus also provide a basis to the whole expression template business). For example, calculating the mean value of an array is an operation which is well defined for any array shape. Why should one have to care about the particular array geometry in the implementation? The answer are iterator objects.

Here's a naive implementation of the general-purpose average:

template<class T,int N>
T average( const MArray<T,N>& A )
{
   T sum(0);
   MArray<T,N>::const_iterator i=A.begin();
   for( ; !i.done(); ++i )
      sum += *i;
   return sum/A.nelements();
}

Usually, one will have much more complicated stuff within the loop... But the example above is enough to get the idea.

As a neat extra feature, the iterators are compatible with those known from the Standard Template Library (STL). So you can use the STL algorithms on MArrays. The only thing to know here is that the standard iterators in the LTL are only models of forward_iterators. That is because they have to deal with arbitrary array geometries such as slices and subarrays with non-unit strides etc., so accessing the n-th element is impossible (in constant time, which we REALLY should).

That's why we provide a second set of iterators which are true random_access_iterators, but only under the precondition that the associated MArray object has a contiguous memory layout (which is always true for newly allocated arrays and for suitable subarrays or slices). The random-access iterators are then simply pointers to the array's data, aka objects of type T*.

The following methods and suitable typedefs for the iterator-types are provided in the class MArray: 

template<class T, int N>
class MArray
{
      ...

      // STL definitions
      typedef T                     value_type;
      typedef T&                    reference;
      typedef const T&              const_reference;
      typedef T*                    pointer;
      typedef const T*              const_pointer;
      typedef size_t                size_type;
      typedef MArrayIter<T,N>       iterator;
      typedef MArrayIterConst<T,N>  const_iterator;
      ...
}

iterator MArray<T,N>::begin();
const_iterator MArray<T,N> begin () const;

Return an iterator for the MArray. These are models of the STL forward_iterator iterator category. The iterator object itself offers the following methods: 

iterator& operator++();
T operator*() const;
T& operator*();
bool operator==( iterator& other );

bool done();    //more efficient than ==end

 iterator MArray<T,N>::end ()

Return an iterator pointing past the end of the MArray. Used with operator== to check for end of iteration. iterator.done() is more efficient, though.

T* MArray<T,N>::beginRA();
T* MArray<T,N>::endRA ();

Return STL compatible random access iterators. Works only under the precondition that the associated MArray object has a contiguous memory layout (which is always true for newly allocated arrays and for suitable subarrays or slices).

With these STL-style random access iterators you can write things like (or anything else using STL algorithms): 

#include <algorithm>
MArray A = ...;
std::sort( A.beginRA(), A.endRA() );

Index Iterators

In many situations one has to fill arrays with values that are expressed as functions of "coordinates" within the array, or more generally, as functions of the array's indices. Imagine setting up initial conditions for a PDE, e.g. a circular sine wave on a 2-d surface. For this purpose index iterators are provided. They behave much like normal iterators, but instead of returning the array's value they return the indices of the element they currently point to. An index iterator can be obtained from an MArray by calling indexBegin():

MArray<T,N> A( ... );
MArray<T,N>::IndexIterator i = A.indexBegin();

 IndexIterator MArray<T,N>::indexBegin ();

Return an IndexIterator for the current MArray.

An index iterator always iterates over the index ranges of the array it was created from. They are used in the same way as normal iterators, except that they have some additional methods and no operator*:

FixedVector I = i(); // get index
int x = i(1);        // get index in first dimension
int y = i(2);        // get index in second dimension

Mostly you will prefer to use the 'automatic' version of the index iterators directly in expressions rather than creating an index iterator by hand and writing out the loop, Array Expressions. These look like an ordinary function in the expression. The "function" simply evaluates to the index of the current element during elementwise evaluation of the expression, e.g.

MArray<float,2> E(10,10);
E = indexPosInt(E,1)==indexPosInt(E,2); // 10x10 unity matrix

While indexPosInt() evaluates to an int, there are also spcialized versions that return float and double values, indexPosFlt() and indexPosDbl(), respectively. These are provided for convenience to avoid having to use cast expressions too frequently.

Array Expressions

Array expressions are expressions involving at least one array-valued operand and returning an array-valued result. They are mostly defined by elementwise application of the operations to the operands (Adding matrices is an example. In contrast, matrix multiplication is an array expression which is not simply defined elementwise).

LTL uses a technique called expression templates (See Todd Veldhuizen's Techniques for Scientific C++; http://extreme.indiana.edu/~tveldhui/papers/techniques/ ) to evaluate such expressions. This technique is used to overcome the problem that would occur if we were simply overloading the functions and operators for arrays, namely that every function or operator would generate a temporary array object to store its result (and that the loop over all elements would be executed once for each operation). In LTL expression evaluation will not generate any temporaries or multiple loops. That means that code like

MArray<float,1> A(...), B(...), C(...), D(...);
D = 2*C + log(A*B);

will be transformed at compile time to something resembling

for( int i=start; i<=end; ++i )
   D(i) = 2*C(i) + log(A(i)*B(i));

In reality this will involve iterators instead of direct indices which will work for any dimensionality and take advantage of some further optimizations that can be performed in special cases, like when the arrays have contiguous memory layout or make use of common strides etc., but the principle is like in the example above. Additionally, the loop gets unrolled automatically by the LTL, and we make sure that the compiler does not assume too loose aliasing constraints on the pointers involved.

As a special bonus, we make use of the vector units present in newer processors (MMX/SSE/SSE2 in x86 compatible processors, Altivec in PowerPC processors). If this feature is enabled (see below), and if all operations used in an expression have vector implementations (on the given hardware platform), LTL will automatically evaluate the loop using the vector unit. This can significantly speed up code execution (espcially on PowerPCs, less so but still worth while on x86).

An expression can contain any mix of the following operands:

If the elements of the MArrays in the expression are of different types, regular C/C++ type promotion rules apply as long as the elements are built-in C++ types. When using user-defined types as elements of MArrays, expressions will still work, but the element types will have to be compatible. As a side effect, when scalars (literals) appear in expressions, these literals will NOT take part in the type promotion process. So while MArray<float> + Marray<double> will be promoted to double, the expression MArray<int> + 1.0f will not.

indexPosInt( const MArray<T,N>& A, const int dim ) expressions are special functions which will evaluate to the index position along dimension dim in the MArray A during each step in the evaluation of the expression.

To fill a 2-d array with a circular sine wave:

MArray<float,2> A( Range(-100,100), Range(-100,100) );
A = sin( sqrt(indexPosFlt(A,1)*indexPosFlt(A,1) +
              indexPosFlt(A,2)*indexPosFlt(A,2)) );

merge( bool_expr, true_case, false_case ) (see Merge Expressions) expressions are a generalization of the A ? T : F pattern. For each element bool_expr is evaluated. If it is true the result is the result of the evaluation of true_case, if not, the result is the result of the evaluation of false_case. When calculating 1/A for example:

MArray<float,2> A( nx, ny ), B( nx, ny );
...
B = merge( A != 0.0, 1.0/A, 0.0 );

If you have a functor object (any object defining operator()), you may use it in any expression using apply(): 

struct myfunc
{
   float operator()( float x )
   {
      // do something with x
      return y;
   }
};

myfunc f;

MArray<float,1> A(N), B(N);
A = ... ;
B = apply( f, A );

An overloaded version of apply() taking 2 arguments is also provided for applying binary functors.

Array Valued Operations

The following binary operators and functions can be used in any array expression:

+, -, *, /,
&&, ||,
&, |, ^,
%,
>, <, >=, <=, !=, ==,
pow(), fmod(), atan2()

and, for convenience, 

+=, -=, *=, /=,
&=, !=, ^=
\endocde

The following array valued unary operators and functions can be used
in any array expression taking arrays and/or expressions as operands:

\code
+, -, !, ~
sin(), cos(), tan(),
asin(), acos(), atan(),
sinh(), cosh(), tanh(),
exp(), log(), log10(),
sqrt(),
fabs(),
floor(), ceil(), round()

Along with some additional handy functions:

// compute integer powers by multiplication
pow2(), pow3(), pow4(), pow5(), pow6(), pow7(), pow8()

If your system provides IEEE math functions, they also can be used:

// IEEE math functions
asinh(), acosh(), atanh(), // inverse hyperbolic
cbrt(),                    // cube root
expm1(), log1p()           // exp(x)-1, log(1+x)
erf(), erfc(),             // error-func and complementary. erf
j0(), j1(), y0(), y1(),    // 1st and 2nd kind bessel functions
lgamma(),                  // natural log of gamma function
rint()                     // rounding etc.

If your compiler and math library fully support the complex<T> type, you may also see the following functions defined:

abs(), arg(), norm(), imag(), real(), conj().

As well as the standard trigonometric, transcendental, exponential, and log functions that extend naturally to complex numbers.

See your system's man pages to see which of the above functions are available and for complete descriptions.

LTL also provides two fucntions to (moderately) safely compare floating point numbers follwoing Knuth, D.E., The art of computer programming, Vol II. 

static inline bool feq( const float a, const float b )
{
   const float ab = fabsf(a-b);
   return  (ab <= 1e-7f*fabsf(a)) || (ab <= 1e-7f*fabsf(b));
}

and the negation fneq(a,b). These can be used in expressions like all other math functions listed above.

Additionally one has the merge() expression and the indexPos() functions described in Array Expressions, and the partial reductions described in Partial Reductions.

Full Reductions

The following scalar valued functions (also called full reductions) are provided for array and expression arguments (See Statistical Functions for MArrays and Expressions reference documentation):

// include statistics.h after marray.h to get these functions
#include <ltl/statistics.h>

Boolean valued reductions:
allof( Expr ), noneof( Expr ), and anyof( Expr ); additionally there is count( Expr ).

All functions below provide an additional instance which neglects an arbitrary NaN value for the calculation of the reduction.

Type T valued reductions:
min( Expr [, T nan] ), max( Expr [, T nan] ), sum( Expr [, T nan] ), and product( Expr [, T nan] ). Minimum, maximum, sum, and product of all values of an expression.

Floating point-valued reductions:

give the average, the variance or standard deviation (and optionally the average in addition), an exact median and a user scalable estimate of the median.

MArray-valued reduction:
histogram ( Expr, int bins, T min, T max [, T nan] ) to build a user defined histogram of an expression.

Kappa-Sigma Clipping:

All these functions do 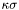$\kappa\sigma$ clipping and return the number of remaining elements after clipping. The resulting mean (average or median) and optionally the final 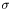$\sigma$ are stored to pointed addresses. For both (median and average results) clipping can be done either according to median and average.

Additionally, we have Tukey's biweight based robust mean and dispersion:

Partial Reductions

These are reductions like the ones in Full Reductions, except that they operate on one dimension only, resulting in a reduction of the rank of their argument by one.

Partial reductions can be used like any other term in expressions, except they cannot be nested, i.e. it is not possible to partially reduce an expression containing another partial reduction without assigning the result of the first reduction to an MArray first.

For example, to assign the sums of the lines of A (2-dimensional) to the corresponding elements of B (1-dimensional length equal to the number of lines in A) do the following:

   // include statistics.h after marray.h to get these functions
   #include <ltl/statistics.h>

      ...

      MArray<T,2> A(5,4);
      A = indexPos(A,1) + 10*indexPos(A,2);

      [[ 11 12 13 14 15 ]
       [ 21 22 23 24 25 ]
       [ 31 32 33 34 35 ]
       [ 41 42 43 44 45 ]]

      MArray<T,1> B(4);

      // partial sum along dimension 1
      B = partial_sum( A, 1 );
      // B = 65, 115, 165, 215;

The following partial reductions are currently implemented for MArray and expression arguments:

See the discussion of the full reductions with the same name for details.

Typecast Operations for Arrays and Expressions

If you assign an expression of a different type to a MArray, or mix operands of different types in an expression, the compiler will probably generate a (long and obscure) list of warnings concerning a possible loss of precision, or assignment of incompatible types.

To avoid that, we provide a cast<type> opearation similar to the static_cast<type> operation in C++ to convert the type of a MArray or Expression in an assignment, or to convert a sub-expression to a different type.

Usage and semantics are (almost) identical to the static_cast<T>() operation. For example, to cast the elements of an MArray<float,2> A to ints, use:

   cast<int>()( A )

See the extra parenthesis to instantiate the cast instance?

To cast a subexpression, use:

      MArray<int,1> A, B;
      MArray<float,1> C, D;
      ...
      B = A + cast<int>()( C/(2.0*D) );

Convolution support in MArray expressions

MArray expression support convolution operations with small kernels. To use this feature, include 

#include <ltl/convolve.h>.

Convolution kernels for MArrays are available implementing various smoothing kernels and finite differences methods that can be used in any MArray expression. Currently, convolutions are implemented for expressions of up to rank 3.

As an example of a declaration of a convolution kernel, let us consider the o(h^2) first derivative along the dimension dim using central differences:

DECLARE_CONVOLUTION_OPERATOR_DIM(cderiv1,A)
    return OFFSET1(A,1,dim) - OFFSET1(A,-1,dim);
END_CONVOLUTION_OPERATOR;

The macros OFFSET0(), OFFSET(i,dim), OFFSET1(i), OFFSET2(i,j), OFFSET3(i,j,k) allow access to elements of an expression relative to the current position. The offsets can be along any one particular dimension, or along dimensions one, two, and/or three (currently, convolutions are only supported in expression up to rank 3). OFFSET0() is short for the current element (element at offset 0). The extent of the convolution kernel (the maximum offsets used in the kernel) are determined automatically for you before the operation is executed. The extent can be different in each dimension and in each direction within a dimension. The convolution will only be evaluated for elements of the operand expression for which the kernel lies completely within the domain of the expression. The elements at the boundary will not be accessed.

This kernel can then be used in expressions:

    MArray<float,2> B, C;
    ...
    B = 1/(2*h) * convolve( C*C/2, cderiv1(dim) );

Which would assign the first derivative along the first dimension of C*C/2 to B.

Note that convolutions can provide higher-order tensors than their operands. An example is the gradient operator: 

MArray<float,2> A(10,10);
MArray<FVector<float,2>,2> B(10,10);
A = 0.0f;
A(5,5) = 1.0f;
B = convolve(A,grad2D());

See the documentation on Convolution support and kernels in MArray expressions for more details and for a list of kernels.

BLAS and LAPACK interface

While the LTL comes with its own implementation of the scalar product dot(), most people will want to use BLAS and LAPACK for more complex linear algebra, especially where optimal performance is important.

LTL provides an interface to use BLAS and LAPACK calls on MArrays of dimension one and two. This interface can be used by

   #include <ltl/marray/blas.h>
   #include <ltl/marray/lapack.h>

These headers can be used independently. blas.h provides BLAS Level 1, 2, and 3 calls on vectors and matrices of float, double, std::complex<float>, and std::complex<double>. lapack.h provides a selection of LAPACK calls. It is very easy to extend it to new calls. See the following snippet for an example and the documentation in these files for details.

   MArray<float,1> x(4);
   ...
   MArray<float,2> A(3,4);
   A = 1,5,9,
       2,6,10,
       3,7,11,
       4,8,12;  // note: column major order ...

   MArray<float,1> y = blas_gemv( A, x );

fftw3 interface

LTL provides an interface to the fftw3 fast fourier transfrom library and provides calls for real and complex transforms of MArrays up to rank 3. See the documentation for fftw.h and the following example:

   #include <ltl/fftw.h>

   // example of 1-dimensional FFT using fftw3 library:
   MArray<double, 1> in(size);
   MArray<std::complex<double>, 1> out(size);
   FourierTransform<double,1> FFT;

   in = 10.0 +
        20.0 * sin(indexPosDbl(in,1) / double(size) * 2.0 * M_PI * 3.0) +
        30.0 * cos(indexPosDbl(in,1) / double(size) * 2.0 * M_PI * 4.0);
   FFT.FFT_Real2Complex(in,out);
   FFT.normalize(out);
   out = merge(real(out * conj(out)) > 1e-9, out, 0);
   std::cout << out << std::endl;

Plotting

Since version 2.0, LTL provides a simple interface to Gnuplot for MArrays and FVectors.

Usage is very simple: 

   #include <ltl/util/gnuplot.h>

   MArray<float,1> A;

   Gnuplot gp;  // start a gnuplot session and open pipe
   Gnuplot gp ("gnuplot-cmd"); // alternative command string

   gp << "plot '-' with lines\n";
   gp.send (A);
   // or
   // gp.send(X,Y)
   // gp.send_iter( v.begin(), v.end() );
   // gp.send_iter( float*, float* );

   double mx, my;
   int mb;
   gp.getMouse(mx, my, mb);

Gnuplot::send() works with MArrays up to dimension 2, FVectors. For stdlib containers use send with any valid iterator range, i.e. send(v.begin(),v.end())

Gnuplot inherits from std::ostream, so any gnuplot commands and data can be sent to Gnuplot via standard streamio operations, operator<<, setprecision(), etc.

Vectorization using MMX/SSE/SSE2 and Altivec

As of LTL version 1.7, LTL is capable of automatically generating code for the vector execution units in modern processors. This is essentially an auto-vectorizer for compilers that do not have this feature (e.g. GCC; also, auto-vectorizing compilers do not generate very useful results most of the time).

If all operations in an expression have vector implementations, LTL can automatically vectorize the execution of the loop over the expression for you. This is controlled via the LTL_USE_SIMD preprocessor macro. If LTL_USE_SIMD is defined (before any LTL includes), LTL will evaluate expressions using the hardware vector unit in the current translation unit. Define the macro LTL_DEBUG_EXPRESSIONS to see which loops in your code actually got vectorized.

Vectorization additionally requires the data to be aligned to vector boundaries in memory. LTL can cope with misaligned arrays, but given the elementwise nature of vector operations, only if all the operands have the same (mis-)alignment can a loop be vectorized. In such a case, the loop will be vectorized with the first elements up to the next vector alignment boundary evaluated in the scalar units. The same applies for arrays with element number which are not divisible by the vector length.

Currently, the vector units in x86 processors (MMX/SSE/SSE2 instructions) are supported, as well as the Altivec unit in PowerPC processors. On PPC platforms, additionally to defining LTL_USE_SIMD, we expect __ALTIVEC__ to be defined. GCC (and IBM xlC on Mac OS X) do so automatically if the -faltivec switch to enable altivec support is provided. On x86, we expect at least SSE2 support to be enabled, and __SSE2__ to be defined, which is accomplished with the -msse2 and/or -msse3 switches with GCC (version 3.4 and above).

Not all operations applicable to MArrays above have vectorized implementations yet, though. (see the file ltl/misc/applicops_altivec.h, ltl/misc/applicops_sse.h, and ltl/marray/reductions_sse.h). Currently, many basic mathematical operations and logical operations are vectgorized, along with many of the statistical reductions. We hope to add more operations over time. Aditionally, under Mac OS X, all operations supported by the vMathLib library are vectorized (this includes most of the starndard math library). Also,

We urge everyone to try out this new feature. But make sure you compare results to the scalar version of your code.

A few caveats to be aware of

While regular C/C++ type promotion applies to array expressions and while many reductions apply their own type promotion (e.g. averages are computed in double no matter what type the data is supplied in), this is NOT the case for vectorized expressions. If you request vectorization in a translation unit YOU have to make sure that (a) all expressions involve only arrays of the same type (to guarantee the same vector length and vector operations) and (b) that it is safe to not promote any types, instead calculate everything in the MArray's element type. Additionally, logical expressions (comparisons) yield different repreresentations of true and false if executed in the vector unit (at least in SSE) compared to a scalar operation. E.g., since the vector unit has only bitwise logical operations, true corresponds to 0xFFFF, or -1, not +1 as in the scalar unit. Since parts of a vectorize expression (the misaligned and the remainder of the iteration count divided by the vector length) will be evaluated in the scalar unit, expect that the result of a logical operation might contain mixed representations of true. False, however is always represented by 0.

If any of these do not apply to your problem DO NOT REQUEST VECTORIZATION.

Vectorization summary

See the files ltl/misc/applicops-altivec.h and ltl/misc/applicops-sse.h to see which operations are vectorized. Additionally, many reductions have vectorized implementations in ltl/marray/reductions_sse.h .

User Defined Operations

Defining one's own functions to be usable in array expressions is pretty easy. There are macros for unary and binary functions which make the matter just a single line of code. Say you have written a function double my_func( double x ) and want this function to be applicable in array expressions:

// here's my function:
inline double my_func( double x )
{
   return x/(1+x*x);
}

// now declare the necessary expression templates:
// the arguments are 'function name' and 'return type'
DECLARE_UNARY_FUNCTION( my_func, double );

If you have a vectorized version of your function you might add the following to the scalar definition above:

// here's the vector implementation of my function:
inline VEC_TYPE(double) my_func_vec( VEC_TYPE(double) x )
{
   ...
}
DECLARE_UNARY_FUNCTION_VEC(my_func, double, my_func_vec);

That's it. Now we can write things like:

MArray<double,2> A(nx,ny), B(nx,ny);
...
B = my_func(2*A+1) * ( ... );

Declaring binary functions is as easy. Use the macro

DECLARE_BINARY_FUNCTION( my_binary_func, return_type );
DECLARE_BINARY_FUNCTION_VEC( my_binary_func, return_type, my_func_vec_impl );

in that case. The vectorized implementation can have any name. It will be associated with the scalar function given as the first argument of these macros.

If you have a functor that defines operator(), you may use it in MArray expressions using apply(). A typical definition of such a functor might look like:

struct functor
{
   typedef float value_type;
   enum { isVectorizable = 1 };

   float operator()( float a )
   {
      return a*a;
   }

   // SSE implementation of float multiply:
   VEC_TYPE(float) operator()( VEC_TYPE(float) a )
   {
      return _mm_mul_ps(a,a);
   }
};

Just set isVectorizable to 0 and leave out the vector implementation if you do not have a vectorzied version of your operation.

To simplifiy writing vectorized code, we provide the following type traits classes and macros:

template<typename T> struct vec_trait
{

   typedef T          value_type;          // The type of the vector's elements
   typedef Tint_type  int_value_type;      // The integer type with the same number of elems per vector
   typedef TTT        vec_type;            // The type denoting the vector itself
   typedef __m128i    arg_type;            // The type of the arguments to the SSE intrinsics
   static inline vec_type init(const T x); // Method returning a vector with all elems set to x
}

With specializations provided for float, double, char, short, int, long long.

And, 

#define VEC_TYPE(T)          vec_trait<T>::vec_type
#define T_VEC_TYPE(T)        typename VEC_TYPE(T)

#define INT_TYPE(T)          vec_trait<T>::int_value_type
#define T_INT_TYPE(T)        typename INT_TYPE(T)

#define INT_VEC_TYPE(T)      VEC_TYPE(typename vec_trait<T>::int_value_type)
#define T_INT_VEC_TYPE(T)    typename INT_VEC_TYPE(T)

#define VARGT(T)             vec_trait<T>::arg_type
#define VARGTLL              VARGT(long long)
#define VEC_INIT(T,val)      vec_trait<T>::init(val)
#define VEC_ZERO(T)          (vec_trait<T>::vec_type)_mm_setzero_si128()
#define T_VEC_ZERO(T)        (typename vec_trait<T>::vec_type)_mm_setzero_si128()

#define VEC_LEN(T)           ((int)(sizeof(VEC_TYPE(T))/sizeof(T)))
#define T_VEC_LEN(T)         ((int)(sizeof(T_VEC_TYPE(T))/sizeof(T)))

#define VEC_UNION(T)         union{ VEC_TYPE(T) v; T a[VEC_LEN(T)]; }
#define T_VEC_UNION(T)       union{ T_VEC_TYPE(T) v; T a[T_VEC_LEN(T)]; }

All of these are defined in ltl/misc/applicops_sse.h.

Array and Expression Conformability

Obviously, array-valued operands and expressions need to be of the same 'shape' if they are to be evaluated by elementwise application of the mathematical/arithmetic/logical operations.

Conformability in LTL is defined as

The index ranges do not matter (yes, I'm aware that this is debatable...). This is mainly a decision driven by pragmatism. If you think of, say, 2-dimensional arrays not only as matrices but also of simply collections of data (images, for example), then you want to be able to add one (part of an) image to another image without worrying about index ranges. Sometimes it's convenient to have images centered around index (0,0), e.g. in the sine wave example in Array Expressions, and still be able to add such an image to (multiple locations in) another image.

Note that there is a caveat here to be aware of. When using index iterators, the index ranges do matter of course, since index iterators always refer to a specific array/expression and therefore iterate over the index ranges of precisely that array/expression.

Various Other Methods

Some methods returning information about or changing the indexing of an MArray. Note that dimensions are counted starting at 1 (what should the zeroth dimension of something be?).

Memory related methods:

Geometry related methods:

Debugging

Range checking for all expressions involving array indexing or subarray creation can be turned on by defining the preprocessor symbol LTL_RANGE_CHECKING before including any LTL header. The system wide default is defined in the file <ltl/config.h>.

#define LTL_RANGE_CHECKING  // turn on range checking
#undef  LTL_RANGE_CHECKING  // turn off range checking [default]

Any range violation will result in either

depending on the following preprocessor symbols:

#define LTL_ABORT_ON_RANGE_ERROR  // abort and coredump [default]
#define LTL_THROW_ON_RANGE_ERROR  // throw RangeException
Generated on 19 Feb 2015 for LTL by  doxygen 1.6.1